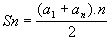Progressão Aritmética (P.A)
► Definição
Podemos chamar de progressão aritmética uma sucessão de termos, tais que a diferença entre um termo qualquer e o seu procedente é constante. Esta diferença é chamada de razão (r).
Uma sucessão aritmética é também chamada de progressão aritmética. Para esta soma indicada dos respectivos termos chama-se de série aritmética.
► Classificação de uma P.A
- Infinita ou Ilimitada:
Se a progressão aritmética tiver um número infinito de termos, pode ser denominada de “infinita ou ilimitada”.
Exemplo:
(8, 10, 12, 14, 16....)
(5, 10, 15, 20, 25....)
(4, 8, 12, 16, 20 ....)
- Finita ou Limitada:
Se a progressão aritmética tiver um número finito de termos, pode ser denominada de “finita ou limitada”
Exemplo:
(6, 8, 10)
(3, 6, 9)
- Em relação à razão (r):
Pode ser:
a) Crescente:
Quando a razão “r” > 0
Exemplo:
(3, 6, 9, 12) ----> r = 3
(2, 4, 6, 8) ----> r = 2
(15, 20, 25, 30) ---> r = 5
b) Decrescente:
Quando a razão “r” < 0
Exemplo:
(6, 4, 2) ---> r = -2
(12, 9, 6, 3) ----> r = -3
(16, 12, 8, 4) ----> r = -4
c) Estacionária:
Quando a razão “r” = 0
Exemplo:
(3, 3, 3) ----> r = 0
(7, 7, 7) ----> r = 0
(5, 5, 5) ----> r = 0
► Notação de uma PA
Observe os termos abaixo:
(a1, a2, a3, a4, ...., an – 1, an)
Logo pela definição, temos o seguinte:
a2 – a1 = a3 – a2 = an – an – 1 = ... = r
Exemplo:
a) (4, 8, 12) é uma PA onde a1 = 4 e r = 4
b) (3, 6, 9) é uma PA onde a1 = 3 e r = 3
► Fórmula do Termo Geral de uma PA
Partindo da definição inicial, temos:
a2 = a1 + r
a3 = a1 + 2r
a4 = a1 + 3r
.
.
.
an = a1 + (n – 1)r
► Propriedades das Progressões Aritméticas
Numa PA, cada termo (a partir do segundo) é a média aritmética dos termos vizinhos deste.
Exemplo:
PA : ( m, n, r ) ; portanto, n = (m + r) / 2
Assim, se lhe apresentarem um problema de PA do tipo:
Três números estão em PA, a forma mais inteligente de resolver o problema é considerar que a PA é do tipo:
(x - r, x, x + r), onde r é a razão da PA.
Numa PA, a soma dos termos eqüidistantes dos extremos é constante.
Exemplo:
PA : ( m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Estas propriedades facilitam sobremaneira a solução de problemas.
► Soma dos n primeiros termos de uma PA
Seja a PA ( a1, a2, a3, ..., an-1, an).
A soma dos n primeiros termos Sn = a1 + a2 + a3 + ... + an-1 + an , pode ser deduzida facilmente, da aplicação da segunda propriedade acima.
Temos: Sn = a1 + a2 + a3 + ... + an-1 + an
É claro que também poderemos escrever a igualdade acima como: Sn = an + an-1 + ... + a3 + a2 + a1
Somando membro a membro estas duas igualdades, vem: Sn = (a1 + an) + (a2 + an-1) + ... + (an + a1)
Logo, pela segunda propriedade acima, as n parcelas entre parênteses possuem o mesmo valor ( são iguais à soma dos termos extremos a1 + an ) , de onde concluímos inevitavelmente que: Sn = (a1 + an).n , onde n é o número de termos da PA.
Daí então, vem finalmente que: