1) Sabendo que o primeiro termo de uma PA é 5 e a razão é 11, calcule o 13o termo:
|
Clique Aqui Para Ver a Resolução: |
|
|
Primeiro devemos coletar todas informações do problema:
a1=5 r=11 a13=?
Para calcular vamos utilizar a fórmula do termo geral, onde an será o a13, portanto n=13. Agora, substituindo:
a13 = 5 + (13 - 1).11
a13 = 5 + (12).11
a13 = 5 + 132
a13 = 137
|
-------------------------------------------------------------------------------------------------------------------------------------------------------------
2) Dados a5 = 100 e r = 10, calcule o primeiro termo:
|
Clique Aqui Para Ver a Resolução: |
|
|
a5 = a1 + (5 - 1).r
100 = a1 + (5 - 1).10
100 = a1 + 40
100 - 40 = a1
a1 = 60
|
-----------------------------------------------------------------------------------------------------------------------------
3) Sendo a7 = 21 e a9 = 27, calcule o valor da razão:
|
Clique Aqui Para Ver a Resolução: |
|
|
a7 = a1 + (7 - 1).r Substituindo pelos valores: 21 = a1 + 6r
a9 = a1 + (9 - 1).r Substituindo pelos valores: 27 = a1 + 8r
Note que temos duas incógnitas (a1 e r) e duas equações, ou seja, temos um sistema de equações. Vamos isolar o a1 na primeira equação e substituir na segunda:
a1 = 21 - 6r
Agora, substituindo na segunda:
27 = (21 - 6r) + 8r
27 = 21 + 2r
27 - 21 = 2r
6 = 2r
6/2 = r
r = 3
|
-----------------------------------------------------------------------------------------------------------------------------
4) (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:
(A) 8a
(B) 7a
(C) 6a
(D) 5a
(E) 4a
|
Clique Aqui Para Ver a Resolução: |
|
|
Informações do problema:
a1 = 23 r = -6 an = -13 n=?
Substituindo na fórmula do termo geral:
an = a1 + (n-1)r
-13 = 23 + (n - 1).(-6)
-13 - 23 = -6n + 6
-36 - 6 = -6n
-42 = -6n Vamos multiplicar os dois lados por (-1)
6n = 42
n = 42/6
n = 7 Resposta certa: Letra "B"
|
-----------------------------------------------------------------------------------------------------------------------------
5) (UCS) O valor de x para que a seqüência (2x, x+1, 3x) seja uma PA é:
(A) 1/2
(B) 2/3
(C) 3
(D) 1/2
(E) 2
|
Clique Aqui Para Ver a Resolução: |
|
|
a1= 2x
a2= x+1
a3= 3x
Neste exercício devemos utilizar a propriedade de uma PA qualquer. Sabemos que o termo da frente é igual ao termo de trás mais a razão. Ou seja:
a2 = a1 + r isolando "r" r = a2 - a1
a3 = a2 + r isolando "r" r = a3 - a2
Como temos "r" igualado nas duas equações, podes igualar uma a outra, ou seja:
a2 - a1 = a3 - a2
Agora, substituindo pelos valores dados no enunciado:
(x + 1) - (2x) = (3x) - (x + 1)
x + 1 - 2x = 3x - x - 1
x - 2x - 3x + x= -1 - 1
-3x = -2 Multiplicando ambos os lados por (-1)
3x = 2
x = 2/3 Resposta certa: Letra "B"
|
-----------------------------------------------------------------------------------------------------------------------------
6) O primeiro termo de uma PA é 100 e o trigésimo é 187. Qual a soma dos trinta primeiros termos?
|
Clique Aqui Para Ver a Resolução: |
|
|
Informações do problema:
a1=100 a30=187 n=30 S30=?
Aplicando a fórmula da soma, temos:
S30 = (100+187).30/2
S30 = (287) . 15
S30 = 4305
|
-----------------------------------------------------------------------------------------------------------------------------
7) Sabendo que o primeiro termo de uma PA vale 21 e a razão é 7, calcule a soma dos 12 primeiros termos desta PA:
|
Clique Aqui Para Ver a Resolução: |
|
|
Informações do problema:
a1=21 r=7 S12=?
Colocando na fórmula da soma, vemos que está faltando um dado. Qual o valor de a12? Então antes de tudo devemos calcular o valor de a12.
a12=a1+(12-1)7
a12=21+77
a12=98
Agora sim, podemos colocar na fórmula da soma:
S12=(a1+a12)12/2
S12=(21+98)6
S12=119 . 6
S12= 714
|
-----------------------------------------------------------------------------------------------------------------------------
8) A soma dos n primeiros termos de uma PA é dada por Sn=n2+2n. O valor do 13o termo desta PA é:
(A) 195
(B) 190
(C) 27
(D) 26
(E) 25
|
Clique Aqui Para Ver a Resolução: |
|
|
Este tipo de questão é clássica, pois tem um pega ratão horrível. Então, vamos esmigalhar ao máximo. Te liga só!
Para calcularmos o 13º termo desta PA, devemos saber o valor do primeiro termo (a1) e o valor da razão, para isso vamos entender o que ele quis dizer com a fórmula dada.
À primeira vista você pode achar que se substituirmos "n" por 13 teremos o valor do 13o termo. Aí está o pega ratão, substitua e veja a resposta da letra "A" (pega ratão).
O que devemos fazer é substituir primeiro "n" por 1, isso dá
S1=12+2.(1)
S1=3
Como S1 significa a soma de todos os termos até a1, ou seja, como não tem nenhum antes de a1 é o próprio valor dele (a1=3)
Se substituirmos "n" por 2, temos:
S2=22+2.(2)
S2=8
Agora tem que se ligar. S2 significa a soma de todos os termos até a2, então é igual à a1+a2. Como já sabemos o valor de a1, logo:
S2=a1+a2=8
3+a2=8
a2=5
Se a1=3 e a2=5 a razão só pode ser 2. Agora podemos achar o 13º termo, é só substituir na fórmula do termo geral:
an=a1+(n-1)r
a13=3+(13-1)2
a13=3+24
a13=27 Resposta certa: Letra "C"
|
-----------------------------------------------------------------------------------------------------------------------------
9) Interpolando 10 meios aritméticos entre 5 e 38, teremos uma PA de razão:
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
|
Clique Aqui Para Ver a Resolução: |
|
|
Interpretando o que é dito: o exercício pede para colocarmos 10 números entre 5 e 38. Assim, teremos:
Como inserimos dez termos no meio dos dois já existentes, a PA terá, 12 termos. Então, as informações deste exercício são:
a1=5 e a12=38 r=?
Agora é só usar a fórmula do termo geral :
a12=a1+(12-1)r
38=5+11r
38-5=11r
33=11r
r=33/11
r=3 Resposta certa: Letra "C"
|
-----------------------------------------------------------------------------------------------------------------------------
10) Quantos meios devemos interpolar entre 112 e 250 para termos uma PA de razão 23?
(A) 3
(B) 4
(C) 5
(D) 6
(E) 7
|
Clique Aqui Para Ver a Resolução: |
|
|
Informações do problema:
a1=112 an=250 r=23
Devemos utilizar a fórmula do termo geral de uma PA:
Aqui que a cobra fuma, meu amigo. A alternativa "E" tá te esperando, pedindo pra tu marcá-la.
7 não é a resposta, é o número total de termos.
Devemos retirar desta contagem os termos 112 e 250, pois é pedido quantos termos devem ser inseridos "ENTRE" estes dois.
Portanto, se no total temos 7 termos, excluindo dois da contagem, temos 5 termos para inserir entre o 112 e o 250.
A resposta certa: Letra "C"
|
-----------------------------------------------------------------------------------------------------------------------------
11) Se numa PA o quinto termo é 30 e o vigésimo termo é 60, qual a razão?
|
Clique Aqui Para Ver a Resolução: |
|
|
a5=30 a20=60 r=?
a20=a5+(20-5).r
60=30+15r
60-30= 15r
r=30/15
r=2
|
-----------------------------------------------------------------------------------------------------------------------------
12) O único valor de x que verifica a equação (x-2)+(x-5)+(x-8)+...+(x-47)=424 é
(A) 51
(B) 41
(C) 31
(D) 61
(E) 71
|
Clique Aqui Para Ver a Resolução: |
|
|
Note que temos uma PA no lado esquerdo da equação com:
a1= (x-2)
a2= (x-5)
Sabemos que é uma PA pois a cada termo estamos somando uma mesma constante (a razão, que no caso é -3). Para descobrir esta razão simplesmente fazemos:
r=a2-a1=(x-5)-(x-2)
r=x-5-x+2 Menos com menos dá mais, por isso temos +2
r=-5+2 X com -X se anulam
r=-3 Esta é a razão
Como os termos estão sendo somados, devemos usar a fórmula da soma dos termos de uma PA. Já sabemos o primeiro termo, o último termo e a razão, mas para usar a fórmula da soma devemos saber o número de termos (ou seja, "n"). Para calcularmos vamos aplicar a fórmula do termo geral no último termo:
an=a1+(n-1)r
Substituindo por seus valores:
(x-47)=(x-2)+(n-1)·(-3)
x-47-x+2= -3n+3
-45-3= -3n
-3n=-48
n=48/3
n=16
Agora sim podemos usar a fórmula da soma:
Sn=(a1+an).n/2
Sn=[(x-2)+(x-47)].16/2
Sn=(2x-49).8
Sn=16x-392
Vamos voltar na equação do exercício e substituir todo lado esquerdo da equação pelo valor calculado:
(x-2)+(x-5)+(x-8)+...+(x-47)=424
16x-392=424
16x=424+392
16x=816
x=816/16
x=51 A Resposta certa: Letra "A"
|
-----------------------------------------------------------------------------------------------------------------------------
13) O sétimo termo de uma PA é 20 e o décimo é 32. Então o vigésimo termo é
(A) 60
(B) 59
(C) 72
(D) 80
(E) 76
|
Clique Aqui Para Ver a Resolução: |
|
|
Informações do problema:
a7=20 a10=32 a20=?
Primeiro vamos colocar todos termos conhecidos na fórmula do termo geral:
a7=a1+6r a10=a1+9r
20=a1+6r 32=a1+9r
Formamos um sistema de equações e resolvemos:
20=a1+6r
32=a1+9r
Vamos isolar o termo a1 na primeira equação:
a1=20-6r
Agora vamos substituir este valor na segunda equação:
32=20-6r+9r
32-20=9r-6r
12=3r
r=12/3
r=4
Agora sabemos o valor da razão, podemos substituir na primeira equação e achar o valor do a1:
20=a1+6·4
20=a1+24
a1=-24+20
a1= -4
Pronto!! Sabemos a razão e o primeiro termo. O exercício pedo o vigésimo. Vamos aplicar a fórmula do termo geral:
a20=a1+19r
a20=-4+19·4
a20=-4+19·4
a20=72
Resposta certa: Letra "C"
|
-----------------------------------------------------------------------------------------------------------------------------
14) (PUC-RS) Na seqüencia definida por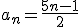 
, a soma dos 10 primeiros termos é igual a:
(A) 
(B)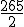 
(C) 53
(D) 265
(E) 53
|
Clique Aqui Para Ver a Resolução: |
|
|
O exercício dá a fórmula do termo geral de uma PA e pede S10. Utilizaremos a fórmula da soma, mas para usá-la devemos saber a1e a10. Estes valores iremos calcular com a fórmula dada pelo exercício:
Agora é só aplicar a fórmula da soma:
Resposta certa: Letra "B"
|
------------------------------------------------------------------------------------------------------------------------------------------------------------
15) (UFRGS) Os números que exprimem o lado, a altura e a área de um triângulo equilátero estão em PA, nessa ordem. A altura desse triângulo mede:
(A)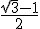 
(B) 
(C) 
(D) 
(E) 
|
Clique Aqui Para Ver a Resolução: |
|
|
Para resolver este exercício devemos ter um conhecimento de Geometria Plana. Este capítulo iremos estudar mais adiante. Mas vamos chamar o lado do triângulo de "L", a fórmula da altura de um triângulo equilátero é  e a área de um triângulo equilátero é . Então, pelo que diz o problema, temos a seguinte PA:
O problema pede o valor da altura, e para isso devemos antes achar o valor de L. Vamos utilizar a propriedade fundamental de uma PA:
Chegamos em uma equação incompleta do segundo grau. Para facilitar os cálculos, coloquei o L em evidência.
Agora é só calcular as raízes, no caso são  e 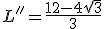 . Como não podemos ter o valor de L como sendo ZERO, então vale só a segunda resposta.
O exercício pede a altura do triângulo, vamos aplicar a fórmula da altura (h):
Nas resposta o problema coloca o 2 em evidência, assim sendo:
Resposta certa: Letra "C"
|
-------------------------------------------------------------------------------------------------------------------------------------------------------------
